কষে দেখি— 2.2 সপ্তম শ্রেণি গণিতপ্রভা সমাধান | Kose Dekhi 2.2 Class 7 Math Solution wbbse

1. সপ্তম শ্রেণির গণিত সমস্ত অধ্যায়ের প্রশ্নোত্তর Click Here

2. সপ্তম শ্রেণির বাংলা সমস্ত অধ্যায়ের প্রশ্নোত্তর Click Here

3. সপ্তম শ্রেণির ইংরেজি সমস্ত অধ্যায়ের প্রশ্নোত্তর Click Here

4. সপ্তম শ্রেণির ইতিহাস সমস্ত অধ্যায়ের প্রশ্নোত্তর Click Here

5. সপ্তম শ্রেণির ভূগোল সমস্ত অধ্যায়ের প্রশ্নোত্তর Click Here

6. সপ্তম শ্রেণির সমস্ত বিষয়ের ইউনিট টেস্ট প্রশ্ন Click Here

কষে দেখি— 2.2 সপ্তম শ্রেণি গণিতপ্রভা সমাধান | Kose Dekhi 2.2 Class 7 Math Solution wbbse

কষে দেখি— 2.2           পৃষ্ঠা সংখ্যা – 30

1. নীচের অনুপাতগুলিকে লঘিষ্ঠ আকারে পরিণত করি ও প্রত্যেকটি অনুপাতের ব্যস্ত অনুপাত লিখি।

(a) 12:15

সমাধানঃ 12:15 = `frac(12){15}` = `frac(4){5}` = 4:5

∴ 12:15 কে লঘিষ্ঠ আকারে প্রকাশ করলে হবে 4:5 এবং তার ব্যস্ত অনুপাত 5:4

(b) 36:54

সমাধানঃ 36:54 = `frac(36){54}` = `frac(2){3}` = 2:3

∴ 36:54 কে লঘিষ্ঠ আকারে প্রকাশ করলে হবে 2:3 এবং তার ব্যস্ত অনুপাত 3:2

(c) 75:120

সমাধানঃ 75:120 = `frac(75){120}` = `frac(5){8}` = 5:8

∴ 75:120 কে লঘিষ্ঠ আকারে প্রকাশ করলে হবে 5:8 এবং তার ব্যস্ত অনুপাত 8:5

(d) 169:221

সমাধানঃ 169:221 = `frac(169){221}` = `frac(13){17}` = 13:17

∴ 169:221 কে লঘিষ্ঠ আকারে প্রকাশ করলে হবে 13:17 এবং তার ব্যস্ত অনুপাত 17:13

(e) 9xy : 12xy

সমাধানঃ 9xy : 12xy = `frac(9xy){12xy}` = `frac(3){4}` = 3:4

∴ 9xy : 12xy কে লঘিষ্ঠ আকারে প্রকাশ করলে হবে 3:4 এবং তার ব্যস্ত অনুপাত 4:3

(f) 429:663

সমাধানঃ 429:663 = `frac(429){663}` = `frac(143){221}` = `frac(11){17}` = 11:17

∴ 429:663 কে লঘিষ্ঠ আকারে প্রকাশ করলে হবে 11:17 এবং তার ব্যস্ত অনুপাত 17:11

(g) 3b : 12c

সমাধানঃ 3b:12c = `frac(3b){12c}` = `frac(b){4c}` = b:4c

∴ 3b : 12c কে লঘিষ্ঠ আকারে প্রকাশ করলে হবে b:4c এবং তার ব্যস্ত অনুপাত 4c:b

(h) 25xyz : 625xyz

সমাধানঃ 25xyz : 625xyz = `frac(25xyz){625xyz}` = `frac(5){125}` = `frac(1){25}` = 1:25

∴ 25xyz: 625xyz কে লঘিষ্ঠ আকারে প্রকাশ করলে হবে 1:25 এবং তার ব্যস্ত অনুপাত 25:1

2. নীচের অনুপাতগুলিকে পূর্ণ সংখ্যার অনুপাতে পরিণত করি ও তাঁর ব্যাস্ত অনুপাত লিখি।

(a) 2.5:12.5

সমাধানঃ 2.5 : 12.5 = `frac(2.5){12.5}` = `frac(25){10}` ÷ `frac(125){10}`= `frac(25){10}` × `frac(10){125}` = `frac(1){5}` = 1:5

(b) `frac(5){8}` : `frac(7){16}`

সমাধানঃ `frac(5){8}` : `frac(7){16}` = `frac(5){8}` ÷ `frac(7){16}`= `frac(5){8}` × `frac(16){7}` = `frac(10){7}` = 10:7

∴ `frac(5){8}` : `frac(7){16}`কে পূর্ণ সংখ্যার অনুপাতে প্রকাশ করলে হবে 10:7 16 এবং তার ব্যস্ত অনুপাত 7:10

(c) 0.7: 0.49

সমাধানঃ 0.7: 0.49 = `frac(0.7){0.49` `frac(7){10}` ÷ `frac(49){100}`= `frac(7){10}` × `frac(100){49}` = `frac(10){7}` = 10:7

0.7: 0.49 কে পূর্ণ সংখ্যার অনুপাতে প্রকাশ করলে হবে 10:7 এবং তার ব্যস্ত অনুপাত 7:10

(d) `frac(2){5}` : `frac(3){4}`

সমাধানঃ `frac(2){5}` : `frac(3){4}` = `frac(2){5}` ÷ `frac(3){4}` = `frac(2){5}` × `frac(4){3}` = `frac(8){15}` = 8:15

∴ `frac(2){5}` : `frac(3){4}`কে পূর্ণ সংখ্যার অনুপাতে প্রকাশ করলে হবে 8:15 এবং 8:15এর ব্যস্ত অনুপাত 8:15

(e) 22 : `4\frac(5){7}`

সমাধানঃ 22 : `4\frac(5){7}` = 22 ÷ `frac(33){7}` = 22 × `frac(7){33}` = `frac(14){3}` = 14:3

∴ 22 : `4\frac(5){7}`কে পূর্ণ সংখ্যার অনুপাতে প্রকাশ করলে হবে 14:3 এবং তার ব্যস্ত অনুপাত 3:14

(f) `frac(7){15}` : `frac(3){20}`

সমাধানঃ `frac(7){15}` : `frac(3){20}` = `frac(7){15}` ÷ `frac(3){20}` = `frac(7){15}` × `frac(20){3}` = `frac(28){9}` = 28:9

∴ `frac(7){15}` : `frac(3){20}`কে পূর্ণ সংখ্যার অনুপাতে প্রকাশ করলে হবে 28:9 এবং 28:9 এর ব্যস্ত অনুপাত 9:28

(g) `1\frac(2){5}` : `frac(7){10}`

সমাধানঃ `1\frac(2){5}` : `frac(7){10}` = `frac(7){5}` ÷ `frac(7){10}` = `frac(7){5}` × `frac(10){7}` = `frac(2){1}` = 2:1

∴ `1\frac(2){5}` : `frac(7){10}`কে পূর্ণ সংখ্যার অনুপাতে প্রকাশ করলে হবে 2:1 সংখ্যার অন এবং তার ব্যস্ত অনুপাত 1:2

(h) 4.4 : 5.61

সমাধানঃ 4.4 : 5.61 = `frac(44){10}` ÷ `frac(561){100}` = `frac(44){10}` × `frac(100){561}` = `frac(4){1}` × `frac(10){51}` = `frac(40){51}` = 40:51

∴ 4.4: 5.61 কে পূর্ণ সংখ্যার অনুপাতে প্রকাশ করলে হবে 40:51 এবং তার ব্যস্ত অনুপাত 51:40

3. নীচের অনুপাতগুলির মিশ্র অনুপাত নির্ণয় করি এবং মিশ্র অনুপাতটি গুরু অনুপাত, লঘু অনুপাত ও সাম্যানুপাত তা লিখি।

(a) 8:6, 3:6 ও 26:13

সমাধানঃ 8:6, 3:6 ও 26:13 অনুপাতগুলির মিশ্র অনুপাত 8 × 3 × 26 : 6 × 6 × 13

= `frac(8 × 3 × 26){6 × 6 × 13}` = `frac(4){3}` = 4:3

4:3 অনুপাতের পূর্বপদ উত্তরপদের থেকে বড়ো। সুতরাং, 4:3 অনুপাতটি গুরু অনুপাত।

(b) `frac(7){5}` : 3, `frac(5){7}` : `1\frac(1){16}` ও 3:16

সমাধানঃ `frac(7){5}` : 3, `frac(5){7}` : `1\frac(1){16}` ও 3:16 অনুপাত গুলির মিশ্র অনুপাত

= `frac(7){5}` × `frac(5){7}` × 3 : 3 × `1\frac(1){16}` × 16

= `frac(3){51}` = 3:51 = 1:17

1:17 অনুপাতের পূর্বপদ উত্তরপদের থেকে ছোটো সুতরাং, 1:17 অনুপাতটি লঘু অনুপাত।

(c) 8:5, 7:12 ও 22:13

সমাধানঃ 8:5, 7:12 ও 22:13 অনুপাত গুলির মিশ্র অনুপাত

= 8 × 7 × 22 : 5 × 12 × 13

= `frac(8 × 7 × 22){5 × 12 × 13}`

= `frac(308){195}` = 308:195

308 : 195 অনুপাতটির পূর্বপদ উত্তরপদের থেকে বড়ো। সুতরাং, 308 : 195 অনুপাতটি গুরু অনুপাত।

(d) `frac(2){3}` : 5, `frac(7){8}` : 2

সমাধানঃ `frac(2){3}` : 5, `frac(7){8}` : 2 অনুপাত দুটির মিশ্র অনুপাত

= `frac(2){3}` × `frac(7){8}` : 5 × 2 = `frac(7){12}` : 10

= `frac(7){12}` ÷ 10 = `frac(7){12}` × `frac(1){10}`

= `frac(7){120}` = 7:120

7:120 অনুপাতটির পূর্বপদ উত্তরপদের থেকে ছোটো। সুতরাং, 7:120 অনুপাতটি লঘু অনুপাত।

4. রীতা 100টি অঙ্কের মধ্যে 60টি সঠিক করেছে। বিনয় ওই অঙ্কে 50 টি সঠিক করেছে। অনুপাতে প্রকাশ করে দেখি কে বেশি অঙ্ক ঠিক করেছে।

সমাধানঃ রীতার করা সঠিক অঙ্ক ও মোট অঙ্কের অনুপাত 60:100 = `frac(60){100}` = `frac(3){5}`

বিনয়ের করা সঠিক অঙ্ক ও মোট অঙ্কের অনুপাত 50:80 = `frac(50){80}` = `frac(5){8}`

`frac(3){5}` ও `frac(5){8}` ভগ্নাংশ দুটির হরের লসাগু- 5×8 = 40

`frac(3){5}` = `frac(3×8){5×8}` = `frac(24){40}` এবং

`frac(5){8}` = `frac(5×5){8×5}` = `frac(25){40}`

যেহেতু, 24 < 25 সুতরাং, বিনয় বেশি অঙ্ক ঠিক করেছে।

5. এবছরে মাধ্যমিক পরীক্ষায় আমাদের বিদ্যালয়ে 150 জন পরীক্ষার্থীর মধ্যে 100 জন গ্রেড A পেয়েছে। পাশের বিদ্যালয়ে 100 জন পরীক্ষার্থীর মধ্যে ৪০ জন গ্রেড A পেয়ে উত্তীর্ণ হয়েছে। এবছর মাধ্যমিক কোন বিদ্যালয়ে গ্রেড A পেয়ে ভালো ফল করেছে তা অনুপাতে প্রকাশ করে বের করি।

সমাধানঃ প্রথম বিদ্যালয়ে গ্রেড A পেয়ে উত্তীর্ণ হয়েছে এমন পরীক্ষার্থীর সংখ্যা ও মোট পরীক্ষার্থীর সংখ্যার অনুপাত 100:150 = `frac(100){150}` = `frac(2){3}`

দ্বিতীয় বিদ্যালয়ে গ্রেড A পেয়ে উত্তীর্ণ হয়েছে এমন পরীক্ষার্থী ও মোট পরীক্ষার্থীর সংখ্যার অনুপাত 80:100 = `frac(80){100}` = `frac(4){5}`

`frac(2){3}` = `frac(2×5){3×5}` = `frac(10){15}` এবং

`frac(4){5}` = `frac(4×3){5×3}` = `frac(12){15}`

যেহেতু 10 < 12 সুতরাং, এবছর মাধ্যমিক দ্বিতীয় বিদ্যালয় (পাশের বিদ্যালয়) গ্রেড A পেয়ে ভালো ফল করেছে।

6. দুটি বাড়ির দামের অনুপাত 4:3 এবং দ্বিতীয়টির দাম 4,20,000 টাকা। প্রথম বাড়িটির দাম কত হিসাব করি। প্রথম বাড়িটির দাম যদি 70,000 টাকা বেশি হতো, তবে তাদের অনুপাত কত হতো দেখি।

সমাধানঃ দুটি বাড়ির দামের অনুপাত 4:3

প্রথম বাড়ির দাম ÷ দ্বিতীয় বাড়ির দাম = 4:3 অর্থাৎ `frac(4){3}`

যেহেতু, 4,20,000 ÷ 3 = 1,40,000

∴ প্রথম বাড়িটির দাম = 4 × 1,40,000 টাকা = 5,60,000 টাকা

প্রথম বাড়িটির দাম 70000 টাকা বেশি হলে প্রথম বাড়িটির দাম হবে (560000+70000) টাকা = 6,30,000 টাকা

∴ এখন প্রথম বাড়িটির দাম ও দ্বিতীয় বাড়ির দামের অনুপাত= 630000:420000
= 3:2

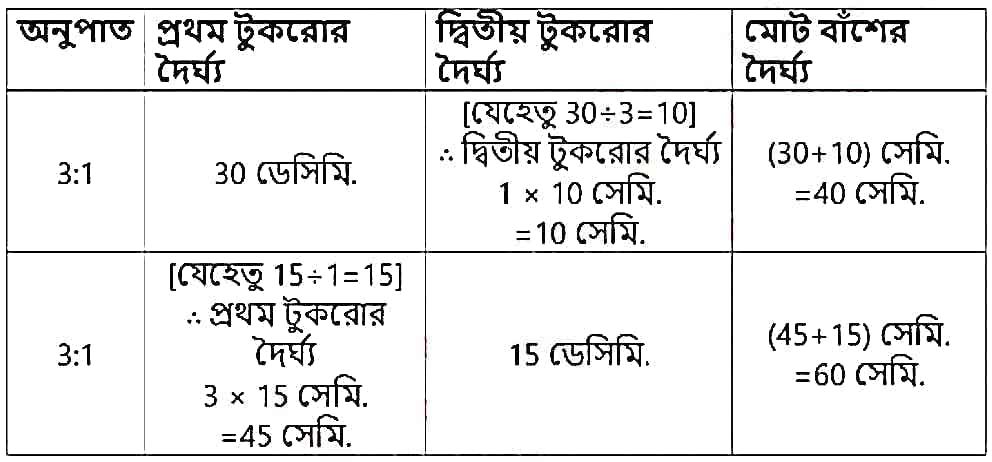
7. একটি বাঁশ থেকে এক টুকরো বাঁশ কেটে নেওয়া হল এবং দেখা গেল দুটি অংশের বাঁশের দৈর্ঘ্যর অনুপাত 3:1। নীচের সারণী থেকে টুকরো দুটির দৈর্ঘ্য কী কী হতে পারে এবং বাঁশটির দৈর্ঘ্য কী কী হতে পারে লিখি।