কষে দেখি— 2.1 সপ্তম শ্রেণি গণিতপ্রভা সমাধান | Kose Dekhi 2.1 Class 7 Math Solution wbbse
1. সপ্তম শ্রেণির গণিত সমস্ত অধ্যায়ের প্রশ্নোত্তর Click Here
2. সপ্তম শ্রেণির বাংলা সমস্ত অধ্যায়ের প্রশ্নোত্তর Click Here
3. সপ্তম শ্রেণির ইংরেজি সমস্ত অধ্যায়ের প্রশ্নোত্তর Click Here
4. সপ্তম শ্রেণির ইতিহাস সমস্ত অধ্যায়ের প্রশ্নোত্তর Click Here
5. সপ্তম শ্রেণির ভূগোল সমস্ত অধ্যায়ের প্রশ্নোত্তর Click Here
6. সপ্তম শ্রেণির সমস্ত বিষয়ের ইউনিট টেস্ট প্রশ্ন Click Here
কষে দেখি— 2.1 সপ্তম শ্রেণি গণিতপ্রভা সমাধান | Kose Dekhi 2.1 Class 7 Math Solution wbbse
কষে দেখি— 2.1 পৃষ্ঠা সংখ্যা – 30
(1) 1 কিগ্রা. চালের দাম 40 টাকা ও 1 কিগ্রা. ডালের দাম 100 টাকা। চাল ও ডালের দামের অনুপাত কত হিসাব করি।
সমাধানঃ
1 কিগ্রা. চালের দাম 40 টাকা
1 কিগ্রা. ডালের দাম 100 টাকা।
চাল ও ডালের দামের অনুপাত = 40 : 100 = 2 : 5
(2) `angleBAC` : `angleABC` : `angleACB` = কত ?
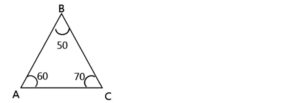
সমাধানঃ `angleBAC` : `angleABC` : `angleACB` = 60 : 50 : 70 = 6 : 5 : 7
(3) 1টি পেন্সিলের দাম ওটাকা ও 1টি লজেন্সের দাম 50 পয়সা। 1টি পেনসিল ও 1টি লজেন্সের দামের অনুপাত করে লিখি।
সমাধানঃ
1টি পেন্সিলের দাম = 3 টাকা = 3×100 পয়সা = 300 পয়সা
1টি লজেন্সের দাম = 50 পয়সা
∴ 1টি পেনসিল ও 1টি লজেন্সের দামের অনুপাত—
= 300 : 50 = 30 : 5 = 6 : 1 (উত্তর)
(4) একটি আধুলি, একটি এক টাকা ও একটি দু- টাকার মুদ্রার মূল্যের অনুপাত লিখি।
সমাধানঃ
1 টি আধুলি = 50 পয়সা,
1 টাকা = 1 × 100 = 100 পয়সা,
2 টাকা = 2 × 100 পয়সা = 200 পয়সা
∴ একটি আধুলি, একটি এক টাকা ও একটি দু-টাকার মুদ্রার মুল্যের অনুপাত—
= 50 : 100 : 200
= 5 : 10 : 20
= 1 : 2 : 4 (উত্তর)
(5) উমার বয়স 12 বছর 6 মাস, রাতুলের বয়স 12 বছর 4 মাস ও নুরজাহানের বয়স 12 বছর হলে, ওদের তিনজনের বয়েসের অনুপাত কত লিখি।
সমাধানঃ উমার বয়স = 12 বছর 6 মাস= (12×12+6) মাস = (144+6) মাস = 150 মাস
রাতুলের বয়স = 12 বছর 4 মাস = (12×12+4) মাস = (144+4) মাস = 148 মাস
নুরজাহানের বয়স = 12 বছর= 12×12 মাস = 144 মাস
∴ ওদের তিনজনের বয়েসের অনুপাত = 150 : 148 : 144 = 75 : 74 : 72
(6) সমকোণী সমদ্বিবাহু ত্রিভুজের কোণগুলির অনুপাত কত লিখি।

সমাধানঃ ধরি, ABC একটি সমকোণী সমদ্বিবাহু ত্রিভুজ
যার `angleBAC` = 90°, AB = AC
এবং `angleABC` = `angleACB` = 45°
∴ সমকোণী সমদ্বিবাহু ত্রিভুজের কোণগুলির অনুপাত
= `angleABC` : `angleBAC` : `angleACB`
= 90 : 45 : 45
= 2 : 1 : 1
অথবা, সমকোণী সমদ্বিবাহু ত্রিভুজের কোণগুলির অনুপাত
= `angleACB` : `angleBAC` : `angleABC`
= 45 : 45 : 90
= 1 : 1 : 2
(7) সমবাহু ত্রিভুজের কোণগুলির অনুপাত কত লিখি।
সমাধানঃ ধরি, ABC একটি সমবাহু ত্রিভুজ
∴ AB = BC = CA
∴ সমবাহু ত্রিভুজের প্রতিটি বাহুর অনুপাত = AB : BC : CA = AB : AB : AB = 1:1:1
(8) পুলকবাবু ও মানিকবাবুর বয়সের অনুপাত 7 : 9; মানিকবাবুর বয়স 72 বছর হলে, পুলকবাবুর বয়স হিসাব করে লিখি।
সমাধানঃ পুলকবাবু ও মানিকবাবুর বয়সের অনুপাত 7 : 9
∴ পুলকবাবুর বয়স ÷ মানিকবাবুর বয়স = 7 ÷ 9
∴ মানিকবাবুর বয়স = `frac7{9}` × 72 বছর = 56 বছর।
(9) দুটি বইয়ের দামের অনুপাত 2:5; প্রথম বইটির দাম 32.20 টাকা হলে, দ্বিতীয় বইটির দাম হিসাব করে লিখি।
সমাধানঃ দুটি বইয়ের দামের অনুপাত 2:5
∴ প্রথম বইটির দাম: দ্বিতীয় বইটির দাম = 2:5
বা, দ্বিতীয় বইটির দাম = 32.20 × `frac5{2}` টাকা = 80.50 টাকা।
(10) বৃত্তের পরিধি ও ব্যাসের অনুপাত 22 : 7; যে বৃত্তের ব্যাসের দৈর্ঘ্য 2 মিটার 1 ডেসিমিটার, সেই বৃত্তের পরিধি হিসাব করে লিখি।
সমাধানঃ বৃত্তের ব্যাস = 2 মিটার 1 ডেসিমিটার = (2×10+1) ডেসিমিটার = (20+1) ডেসিমিটার = 21 ডেসিমিটার।
বৃত্তের পরিধি ও ব্যাসের অনুপাত 22 : 7
∴ বৃত্তের পরিধি ÷ বৃত্তের ব্যাসের = 22 ÷ 7
∴ বৃত্তের পরিধি = `frac(22){7}` × 21 = ডেসিমিটার = 66 ডেসিমিটার = `frac(66){10}` মিটার = 6.6 মিটার = 6 মিটার 6 ডেসিমিটার।
(11) আমাদের সপ্তম শ্রেণিতে 150 জনের মধ্যে 90 জন ও ষষ্ঠ শ্রেণিতে 140 জনের মধ্যে ৪০ জন অঙ্কন প্রতিযোগিতায় নাম দিয়েছে। অনুপাতে প্রকাশ করে দেখি কোন শ্রেণিতে প্রতিযোগী বেশি।
সমাধানঃ সপ্তম শ্রেণিতে মোট ছাত্রছাত্রী ও অঙ্কন প্রতিযোগিতায় নাম দেওয়া ছাত্রছাত্রীর অনুপাত = 150 : 90 = 5 : 3
∴ অঙ্কন প্রতিযোগিতায় নাম দেওয়া ছাত্রছাত্রীর আনুপাতিক ভাগহার = `frac(5){5 + 3}` = `frac(5){8}`
ষষ্ঠ শ্রেণিতে মোট ছাত্রছাত্রী ও অঙ্কন প্রতিযোগিতায় নাম দেওয়া ছাত্রছাত্রীর অনুপাত= 140 : 80 = 7 : 4
∴ অঙ্কন প্রতিযোগিতায় নাম দেওয়া ছাত্রছাত্রীর আনুপাতিক ভাগহার = `frac(4){7 + 4}` = `frac(4){12}`
এখন, `frac(5){8}` = `frac(5 × 11){8 + 11}` = `frac(55){88}` এবং `frac(4){11}` =
`frac(4 × 8){11 + 8}` = `frac(32){88}`
∴ সপ্তম শ্রেণিতে প্রতিযোগী বেশি।
(12) দুটি সংখ্যার অনুপাত 5 : 7 এবং সংখ্যাদুটির গ. সা. গু. 13 হলে সংখ্যাদুটি কী কী ?
সমাধানঃ দুটি সংখ্যার অনুপাত 5 : 7 এবং সংখ্যাদুটির গ. সা. গু. 13
∴ প্রথম সংখ্যাটি হল 5×13 = 65 এবং দ্বিতীয় সংখ্যাটি হল 7×13 = 91
